I first discovered percolation theory about a year ago and was instantly fascinated.  I now consider it to be one of the deepest subjects in science.

The percolation of water.
Percolation theory is named after percolation, which is the flow of water through a porous medium, such as coffee grinds. To get acquainted with this, let us consider a rock which has many small cavities. Let us assume the cavities are spherical and randomly distributed. An interesting question to ask is:

“At what volume fraction of cavities does the rock become permeable?”

This question can be phrased in a more precise way:

“Let us randomly place spherical cavities of radius r in a medium, allowing them to overlap. At what volume fraction of cavities is water able to travel arbitrarily long distances through the medium?”percolation_exA way to visualize this is to picture a slab of this rock, with a thickness L, covered with water on top. The rock extends infinitely to the left and right. At a certain critical volume fraction, called the percolation threshold, water will always be able to find a path through the rock, regardless of the thickness L.

For this simple example, the solution for the critical volume density is easy to guess. If you guessed that the critical volume threshold is ½ , you would be wrong! The threshold (in 3 dimensions) is actually:

0.289573 +/- .000002

In other words, when the cavities start to occupy ~28% of the volume, a path is always possible. I am not sure what I found more startling – the fact that the threshold is so low, or the fact that nobody has been able to prove exactly what the threshold is!  The threshold is determined using a computer simulation, but computers can only simulate finite systems. Thus, there is an uncertainty in the number!

Part of the “deepness” of percolation theory is that it is filled with extremely simple mathematical questions which have never been solved. Even more startling is the fact that (as far as I can tell), mathematicians don’t even have a very good idea about how to even start a solution! Thus we see that from this mundane looking physical process (sorry geologists!) a deep puzzle emerges.

Percolation on lattices.
In our previous example we considered cavities distributed arbitrarily through space. It was an example of what is called continuum percolation. Some other example percolation thresholds for continuous percolation can be found on Wikipedia.

Most of the percolation theory written down so far deals with percolation on lattices. For instance, consider a square grid.  The chance that a given square is a “cavity” is a fixed probability, P. Using an applet from Wolfram Demonstrations, I generated the following pictures:

percolation_squaresTo the best of our knowledge, the percolation threshold on the square lattice is:

P_c  = 0.59274605(3)

With the applet, I was able to get percolation at P = .58, but that was with a finite system. If I had made the system larger, percolation wouldn’t have occurred until P = .59…

Site percolation vs. bond percolation

The type of example I just gave is an example of site-percolation. In bond percolation, we picture ‘water’ moving along along bonds/edges rather through sites/squares.

Let us adopt the more general terminology. Instead of referring to ‘cavities’, let us call them ‘sites’.  Edges are called ‘bonds’. A series of connected sites is called a ‘cluster‘. At the percolation threshold, clusters of infinite size exist.

The following table I compiled shows site and bond percolation thresholds for some simple lattices: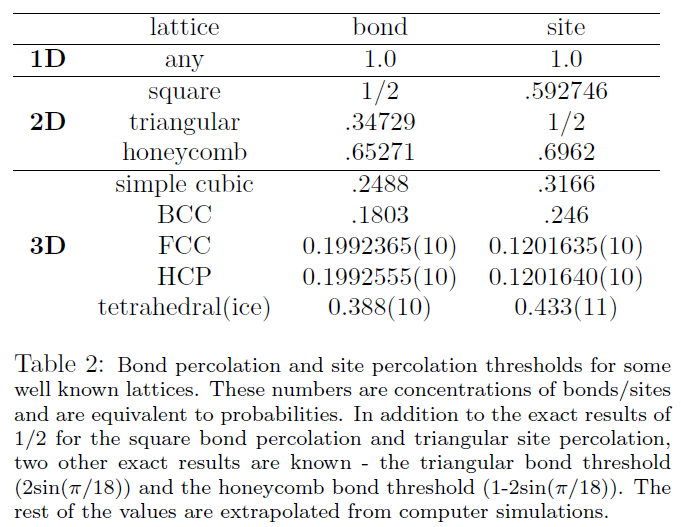percolation_thresholdsA few of these are known exactly, but most are not.

Just to whet your appetite further for his subject, here are some interesting facts about the types of clusters which appear at the percolation threshold:

— Clusters exhibit fractal scaling and fractal shapes.

— The distribution of cluster sizes follows a power law, with a ‘fat’ tail.

And to set your mind spinning, here are some examples of percolation thresholds in nature:

— enough cracks form in rock, allowing trapped natural gas to be extracted (“fracking”).

— a disease starts to spread along a social network when the average number of social interactions per person reaches a certain number.

—  A language is taken up by a critical fraction of well-connected speakers, allowing it to dominate all other languages in a certain geographic area.

— galactic matter reaches a critical density, allowing the formation of stars and galaxies.

— the probability of chemical bonding reaches a critical value, causing a liquid to turn into a gellatin at a certain temperature.

— A heterogeneous material becomes conductive when the metallic fraction reaches a certain threshold.

A good book on this subject is “Introduction to Percolation Theory” by Dietrich Stauffer and Ammon Aharony. It’s one of those books which I’d love to read in full if I had more free time.