Recursion is something that many computer science majors consider elegant. However, in simulation, speed far outweighs how many lines of code are underneath. [That is one reason why physicists still code in Fortran.]

I recently did some fooling around with recursive algorithms in Python. They are viewable at https://github.com/delton137/python_tests

To time different functions, I created a function for timing:

#----time a function -------------------------------------------------
def time_funct(function, args, output=False):
	t0 = time.time()
	result = function(args)
	t1 = time.time()
	ElapsedTime = t1-t0
	if output: print("%25s: %i  time: %8.2e seconds" % (function.__name__, result, ElapsedTime) )
	return ElapsedTime

Next, a function for timing a list of functions of the form f(N) for different N and making a nice log-log plot:

#----given list of functions of form f(n), plot scaling with n -------
def plot_scaling(functs_to_test,num_tests=20,max_value = 1000,max_time  = .1):
	'''Inputs:
		functs_to_test : list of unctions
		num_tests      : number of tests to perform type:int
		max_value      : maximum value to test type:int
		max_time       : maximum time in seconds
	'''
	nvalues = floor(logspace(1, log10(max_value), num_tests))
	times = zeros(num_tests)

	for f in functs_to_test:
		for i in range(num_tests):
			times[i] = time_funct(f, int(nvalues[i]))

			#if (type(f) == "__main__.memoized"):
			#f.cache = {}

			#if runtime is becoming too long, bail out of the test
			if (float(times[i]) > max_time):
				break 	

		plt.loglog(nvalues, times, "-", label=f.__name__)
	plt.legend()
	plt.xlabel("value")
	plt.ylabel("time (s)")
	plt.show()

Now let’s compare some ways of calculating the Fibonacci sequence. First we have the normal recursive method:

#--- normal recursive Fibonacci number calculator -------------
def recursive_fib(n):
  if n < 2:
    return 1
  else:
    return recursive_fib(n-1) + recursive_fib(n-2)

The problem with recursion is that it involves many redundant calls (see this this tree structure to see why), which causes the Fibonacci calculation to scale exponentially with N. This can be solved with memoization, which means you store previously calculated values in a lookup table (cache) so they can be used if the function is called again. In Python you can memoize a function with the memoization decorator:

import collections
import functools

class memoized(object):
   '''Decorator. Caches a function's return value each time it is called.
   If called later with the same arguments, the cached value is returned
   (not reevaluated).
   Taken from the python decorator library: https://wiki.python.org/moin/PythonDecoratorLibrary#Memoize
   '''
   def __init__(self, func):
      self.func = func
      self.cache = {}
      self.__name__ = func.__name__
      self.func_name = func.func_name #python2 support

   def __call__(self, *args):
      if not isinstance(args, collections.Hashable):
         # uncacheable. a list, for instance.
         # better to not cache than blow up.
         return self.func(*args)
      if args in self.cache:
         return self.cache[args]
      else:
         value = self.func(*args)
         self.cache[args] = value
         return value
   def __repr__(self):
      '''Return the function's docstring.'''
      return self.func.__doc__
   def __get__(self, obj, objtype):
      '''Support instance methods.'''
      return functools.partial(self.__call__, obj)</pre><pre>
#--- memoized recursive Fibonacci number calculator -------------
@memoized
def memoized_recursive_fib(n):
  if n < 2:
    return 1
  else:
    return memoized_recursive_fib(n-1) + memoized_recursive_fib(n-2)

Next we have simple iteration:

#--- simple iteration -------------------------------------------
def iter_fib(n):
	if n < 2:
		return 1
	rnm1 = 2
	rnm2 = 1
	for i in xrange(n-2):  
		rn = rnm1 + rnm2
		rnm2 = rnm1
		rnm1 = rn
	return rn

Next we have matrix representation:

#--- iteration using matrix multiplication ----------------------
M = matrix([[1, 1], [1, 0]])
def matrix_iter_fib(n):
  if n < 2:
    return 1
  MProd = M.copy()
  for i in xrange(n-2):
    MProd *= M
  return MProd[0,0] + MProd[0,1]

Finally, just for fun, the direct computation:

#--- direct computation ------------------------------------------
def direct_fib(n):
	s5 = sqrt(5)
	return int( (1/s5)*( ((1 + s5)/2)**(n+1) - ((1 - s5)/2)**(n+1) ) )

now we run:

functs_to_test = [recursive_fib,
                  memoized_recursive_fib,
                  iter_fib,
                  matrix_iter_fib,
                  direct_fib]
plot_scaling(functs_to_test)

We obtain

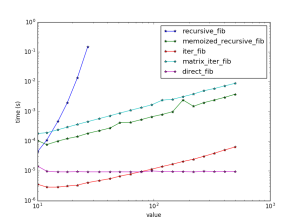
fib_tests

As expected, the pure recursive method scales as exp(N). The memoized method linearly but uses significant memory [log(N)]. The iterative method has the same scaling but is almost 100x faster!

As a side note, the maximum recursion depth in Python is set very low. I had to use the following to increase it:

import sys
sys.setrecursionlimit(10000)

Now let’s do another very common recursive problem – the ‘making change’ problem. Given a target amount N, how many ways are there to make change, if you have an unlimited number of coins with denominations in the set {1,5,10,25}? The recursive algorithm tries subtracting all possible combinations from the target amount and sees if any of them work:

#-----------recursive solution----------------------     
def rec_count(remainder):
     if remainder == 0:
          return 1.0
     if remainder > 0:
          pass
     if remainder < 0:
          return 0
     return sum(rec_count(remainder - coins) for coins in coins)

The iterative solution starts from N=1, and then builds up to N=N:

#----------------iterative solution-------------------------------
def iter_count_ways(N):
     global coins
     num_coins = len(coins)
     ways = zeros(N+1)

     ways[0] = 1

     #build up each row
     for j in range(1,N+1):
          for coin in coins:nbsp;     
               if ((j - coin) >= 0):     
                    ways[j] += ways[j - coin]
     return ways[N]

Now let’s test them:

functs_to_test = [rec_count, rec_count_memoized, iter_count_ways]
plot_scaling(functs_to_test)

c

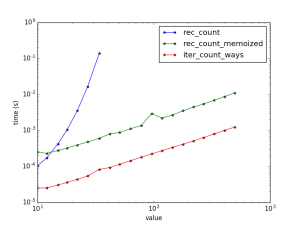coins_problem_tests<figcaption>Speeds and scaling for coins problem.</figcaption></figure>

Now I should note that in these tests I am resetting the memoization cache for each new test N. If you don’t reset the cache and reuses it for each successive test, somewhat surprisingly one obtains only a slight speedup: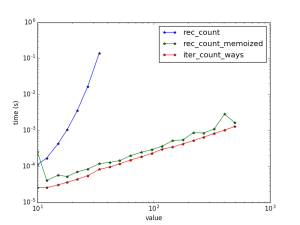coins_problem_tests_cache

I thought this may be due to the fact that the test points are logarithmically spaced, but it appears not.

Memoization makes recursion palatable, but it seems iteration is always faster.

It is worth mentioning that iterative methods can be memorized as well – any function that may be called repeatably can.  For instance, I memoized the iterative method: it keeps all the values it has computed so far, and then picks up where it left off when asked to compute a value that is not already stored:

#----------------memoized iterative solution----------------------
wayscache = {0:1}
maxcached = 0
def iter_count_ways_memoized(N):
     global coins
     global wayscache
     global maxcached

     if (N < maxcached):
          return wayscache[N]
     else:
          for j in range(maxcached,N+1):
               wayscache[j] = 0
               for coin in coins:          
                    if ((j - coin) >= 0):      
                         wayscache[j] += wayscache[j - coin]
          maxcached=N
     return wayscache[N]

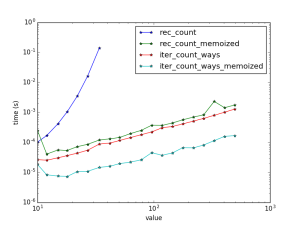
coins_problem_tests_memoized_iter

 

Although recursive methods run slower, they sometimes use less lines of code than iteration and for many are easier to understand. Recursive methods are useful for certain specific tasks, as well, such as traversing tree structures.